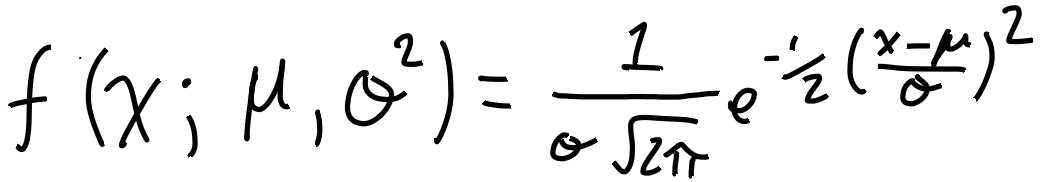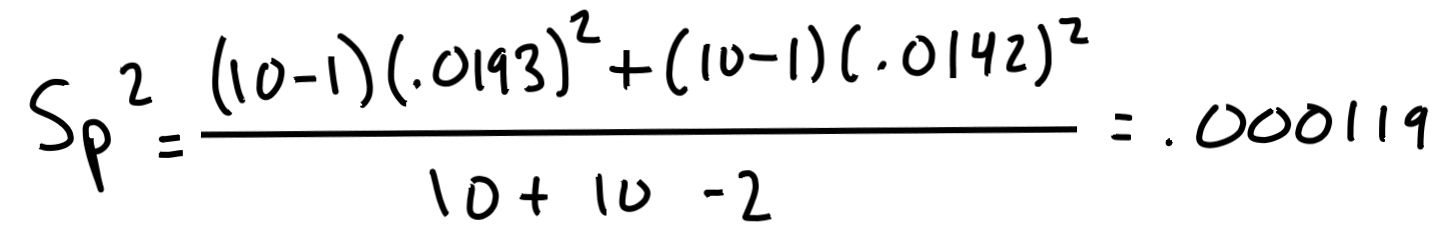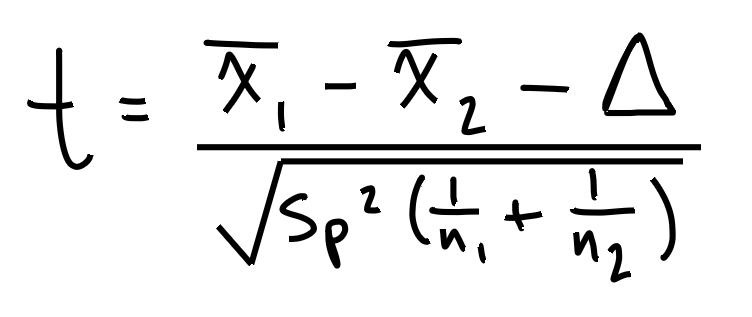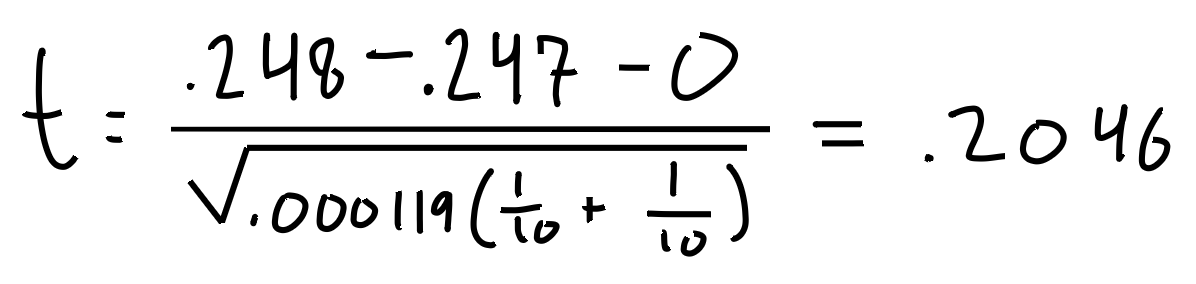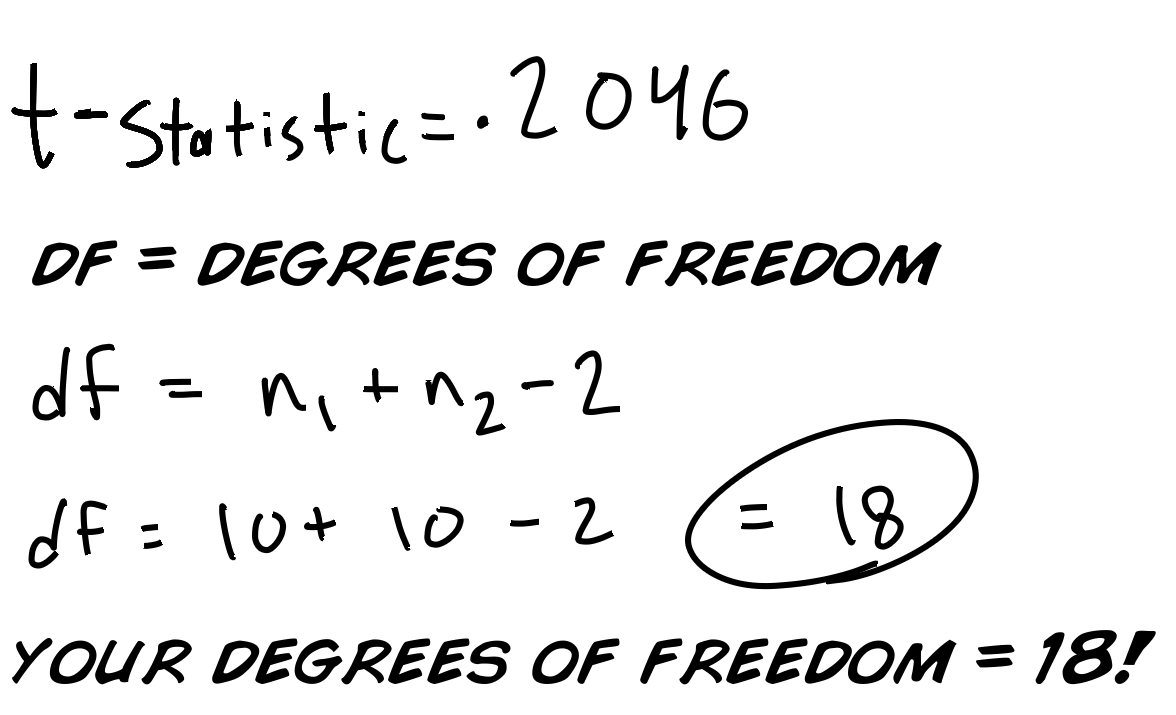Experiment: Entlarv' den P-Wert durch die Macht der Statistik
In den meisten unserer Experimente bei Backyard Brains sammeln wir Daten. Du fragst dich vielleicht: "ja toll, aber was mach ich eigentlich mit den vielen Zahlen?" Willkommen in der wunderbaren Welt der Statistik. In dieser Unterrichtsstunde werden wir dir erklären wie wir eine Hypothese aufstellen können und was man alles mit Daten anstellen kann nachdem man sie erhoben hat. Du hast noch nie Daten erhoben und weißt gar nicht was das bedeutet? Gar kein Problem, du kannst die Daten einfach während diesem Experiment sammeln oder bereits existierende nehmen. Du hast die Wahl.
Was lernt man hier?
Du wirst lernen wie man eine Hypothese aufstellt. Sobald du Daten hast, wirst du lernen wie man diese analyziert indem wir statistische Testverfahren anwenden. Diese sind fundamental um zu beweisen ob deine Resultate deine Nullhypothese unterstützen oder über den Haufen werfen (das wäre dann die Testhypothese).
Voraussetzung
- Reaktionszeit
- Nervengeschwindigkeitsrennen
Du solltest bereits ein Datenset erhoben haben. D.h. du brauchst Zahlen, die du miteinander vergleichen kannst. Falls du noch kein Experiment gemacht hast, in dem du ein Datensatz erhoben hast, kannst du einfach eins der beiden unten gelisteten Experimente machen. Du kannst auch unseren Datensatz über die Reaktionszeiten von Links- und Rechtshändern verwenden, indem du dieser Anleitung folgst.
Ausrüstung
Hintergrund
In fast jedem Experiment sammelt man Datenpunkte. Diese beschreiben eine Beobachtung/Messung. Oft reichen aber Beobachtungen nicht aus, denn man muss auch zu Schlussfolgerungen kommen. Dann werden sie zu unterschiedlichen Zeitpunkten (oder Umständen) miteinander verglichen. Beobachten ist einfach. Man sieht mal jemanden mit Locken, dann jemanden mit braunen Augen. Eine Folgerung daraus zu ziehen ist aber sehr schwierig. Deswegen benötigen wir eine gut durchdachte Datensammlung und eine elegante Analyse. Ein Beispiel: Wie würdest du die Durchschnittsgröße des Menschen bestimmen? Um das herauszufinden würdest du wohl kaum ausschließlich zu einem Basketballteam oder auf die Pferderennbahn zu den Jockeys gehen? Oder?
Einen Schritt weiterzugehen und zwei Populationen miteinander zu vergleichen ist sogar noch schwerer. Kann man ganz leicht beweisen, dass Männer im Durchschnitt größer sind als Frauen? Sehr viele Variablen können dazu beitragen, dass du keine richtige Folgerung schließt. Wenn wir nur die Körpergröße von Basketballdamen und männlichen Jockeys vergleichen haben wir nicht nur einen winzigen Datensatz, sondern eine voreingenommene Tendenz (wir verfälschen das Ergebnis!). Ebenfalls wichtig: Sind die Daten professionell erhoben oder aus eigenen Angaben?
Wie du dir jetzt vielleicht vorstellen kannst ist es harte Arbeit "gute" Daten zu sammeln und zu analysieren. Die guten Nachrichten zuerst: gute Statistiker sind mehr als gefragt heutzutage.
In dieser Stunde werden wir grundlegende, statistische Analysen durchführen. Zuerst müssen wir uns aber auframmen und ein paar Daten erheben/aufnehmen/sammeln. Du hast Glück, wenn du bereits eines unserer kognitiven Experimente gemacht hast, denn dann hast du schonmal ein paar Daten mit denen du arbeiten kannst. Wir hoffen du hast deine Kontrollexperimente sorgfältig ausgewählt und gewissenhaft durchgeführt! Verwende ruhig deine Daten, oder erhebe einfach neue. Falls deine Stichprobenzahl unter 7 Leuten liegt bei deinen Experimenten, solltest du noch mehr Daten erheben.
Die Hypothese
Bevor wir Daten sammeln müssen wir Hypothesen aufstellen.
"Rohe Daten", Graphen & Verteilungen
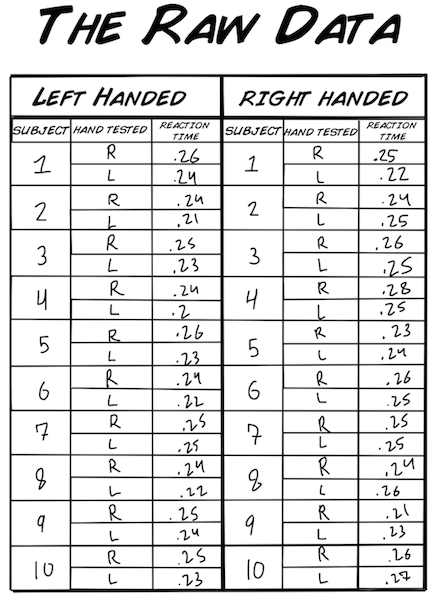
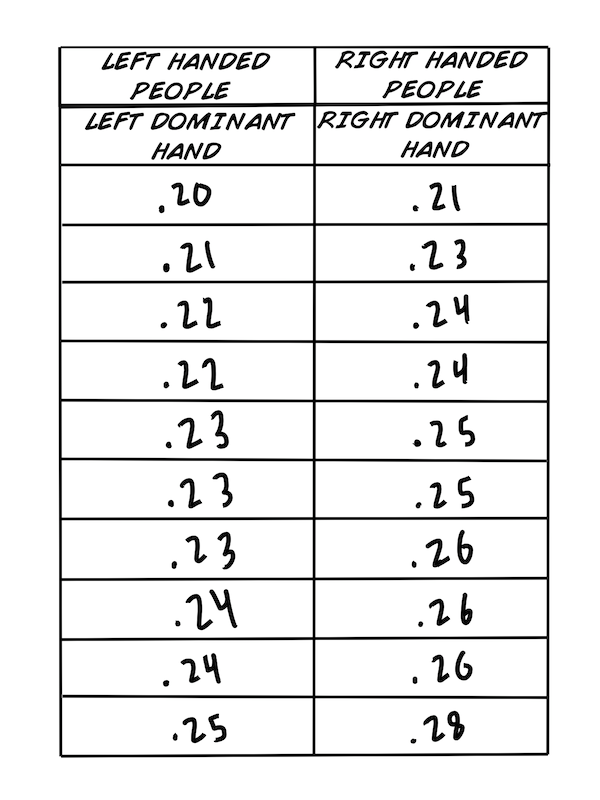
Unten findest du ein Datenset, das wir aufgenommen haben während dem Experiment:Reaktionszeit! Das sind die Reaktionszeiten für sowohl linke als auch rechte Hände auf einen visuellen Reiz (Aufleuchten einer Lampe). Wir haben für unsere Stichprobe Schüler gleichen Alters ausgesucht, 10 Linkshänder und 10 Rechtshänder. Die Reaktionszeit wird in Sekunden festgehalten.
So, jetzt haben wir die "Rohdaten" und können anfangen uns die Daten mal anzuschauen. Es scheint das keine "komischen" Werte in unserem Datensatz vorkommen, das heißt, dass wir wohl eine gute Stichprobe gesammelt haben. Ein mögliches Gegenbeispiel: Falls einer der Werte .78 (=0.78s) wäre, dann scheint bei dieser Messung etwas schief gegangen zu sein. So einen Wert würden wir aus unserem Datenset werfen. Klingt aber auch ein bisschen "komisch", oder? Einfach etwas nicht zu berücksichtigen. Das stimmt, aber diese in der Mathematik als "Ausreißer" beschriebenen Werte verfälschen die Analyze und können durch Statistiktests erkannt werden. Es ist allerdings extrem wichtig zu hinterfragen, ob es sich bei den Ausreißern um Messfehler oder reelle Ergebnise handelt. Wenn ihr mehr darüber lernen wollt, klickt auf die Wikipediaerklärung.
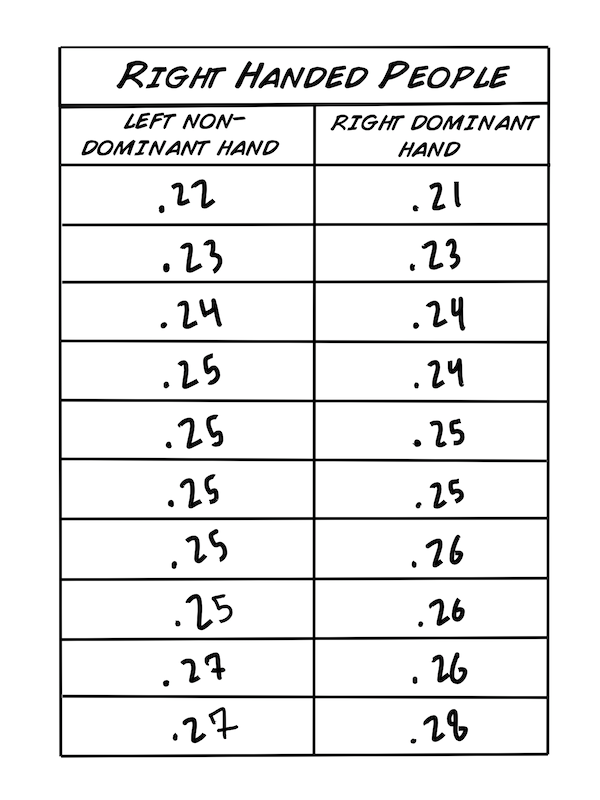
Als nächstes wollen wir unsere Daten so sortieren, dass wir sie untersuchen können um unsere beiden Hypothesen zu testen:
Hypothese 1: Rechtshänder sind schneller mit ihrer rechten, also ihrer dominanten Hand.
Hypothese 2: Linkshänder sind im Allgemeinen schneller als Rechtshänder.
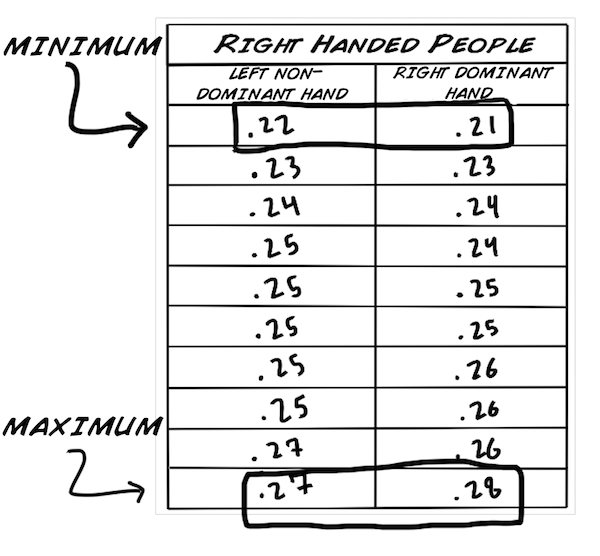
Wir haben die Werte in aufsteigender Reihenfolge sortiert, weil es so einfacher ist mit den Daten zu arbeiten. Bevor wir statistische Tests anwenden müssen wir ein paar grundlegende Werte berechnen.
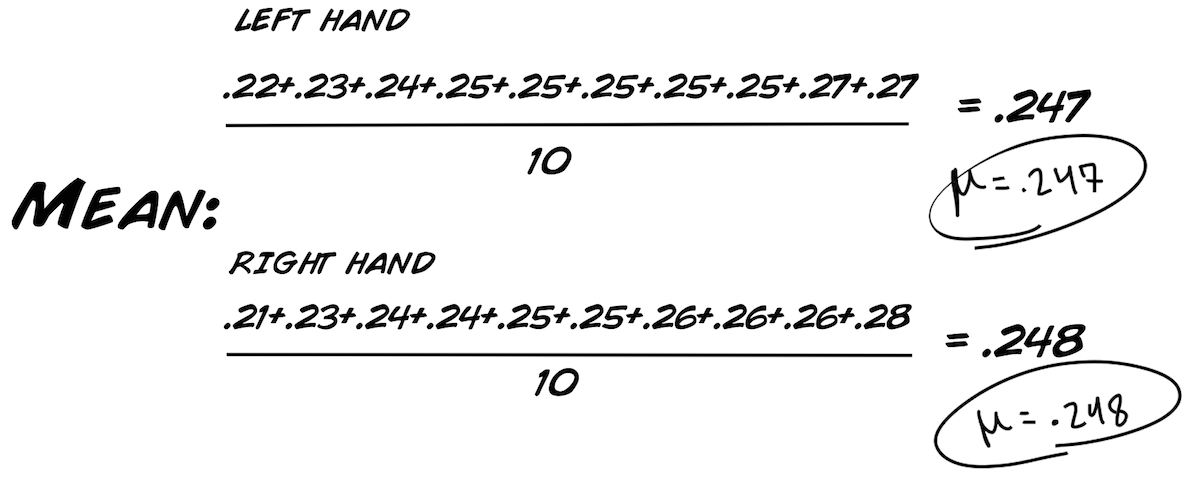
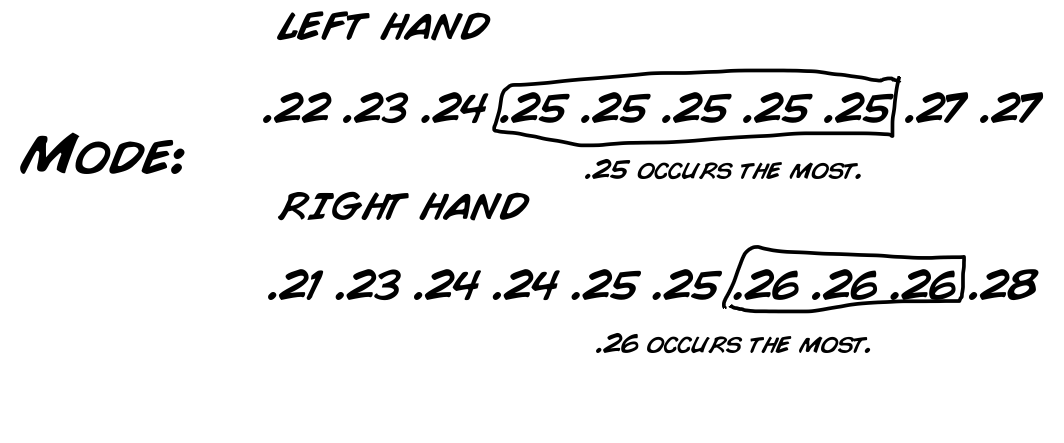
Als erstes wollen wir diese grundlegenden Werte für unseren Datensatz berechnen:
Das sind interessante Resultate.
Wir haben hier die Werte für unsere erste Hypothese mit dem ersten Datensatz berechnent und du kannst nun das Gleiche für unsere zweite Hypothese machen.
Sobald wir irgendwelche Folgerungen über die Reaktionszeiten von Rechts- und Linkshändern machen wollen, müssen wir unsere Daten graphisch visualisieren und statistische Tests durchführen. Zuerst lernen wir etwas über Wahrscheinlichkeitsverteilungen bevor wir mit den Statistiktests loslegen.
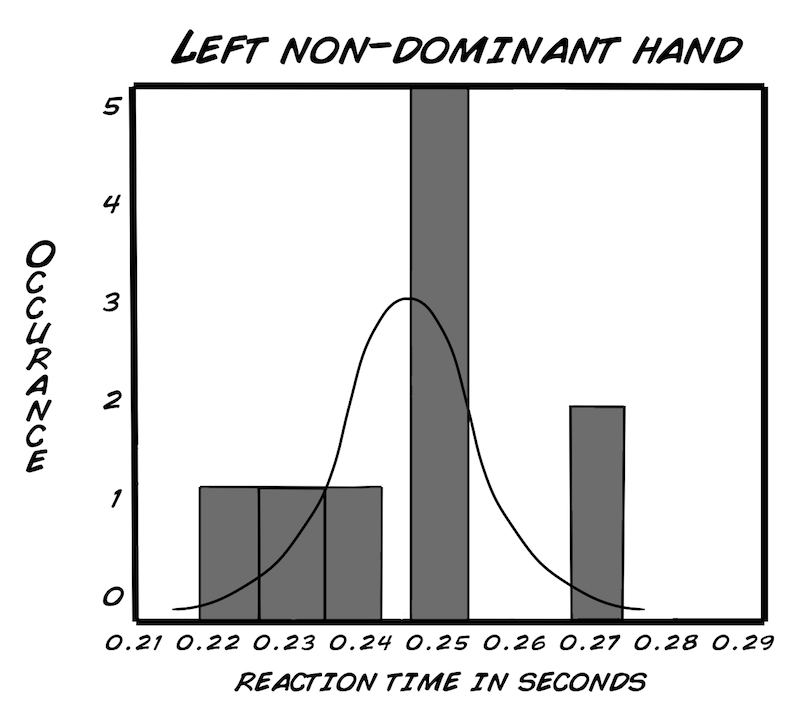
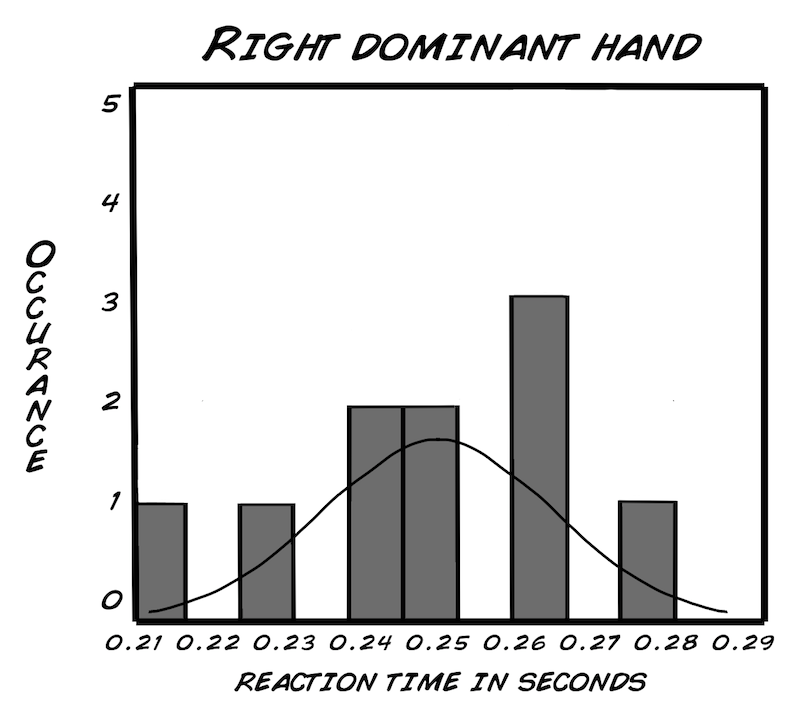
Als Erstes werden wir ein "Histogramm" erstellen, so können wir die Daten besser untersuchen. Die Dichte oder die Anzahl des Vorkommens wird unsere y-Achse. Die x-Achse ist der Bereich, der von den Werten unserer Daten abgedeckt wird. Die Kurve um unser Histogramm ist die "Normalverteilungskurve". Sie ist eine Art von Wahrscheinlichkeitsverteilung. Was ist eine Wahrscheinlichkeitsverteilung? Es ist eine Gleichung oder Tabelle mit Werten, die unsere Ergebnisse verbindet (in unserem Fall, Reaktionszeit), abhängig von der Wahrscheinlichkeit, dass dieser Wert vorkommt. Am besten du schaust dir die Histogramme mal an (unten für die Rechtshänder). Mach' dein eigenes Histogramm für die Linkshänder mit einem Programm wie Excel oder einer open-source Alternative (OpenOffice etc.). Frag' am besten deinen Lehrer oder befreundeten Wissenschaftler aus deiner Nachbarschaft, ob er dir dabei helfen kann, wenn's nicht klappt. Vergiss' nicht: Übung macht den Meister und nicht voreilig aufgeben!
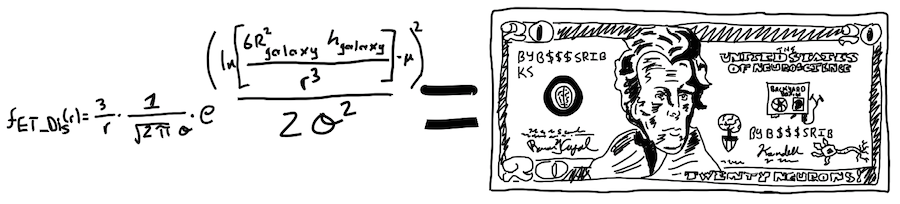
Es gibt sehr viele Wahrscheinlichkeitsverteilungskurven auf dieser Welt, aber wir benutzen die "Normalverteilung", da sie am meisten verwendet wird und für die menschliche Reaktionszeit am besten geeignet ist. Was heißt normalverteilt? Hier handelt es sich um ein mathematisches Model einer "normalen" Abweichung. Hier kommt die Formel:
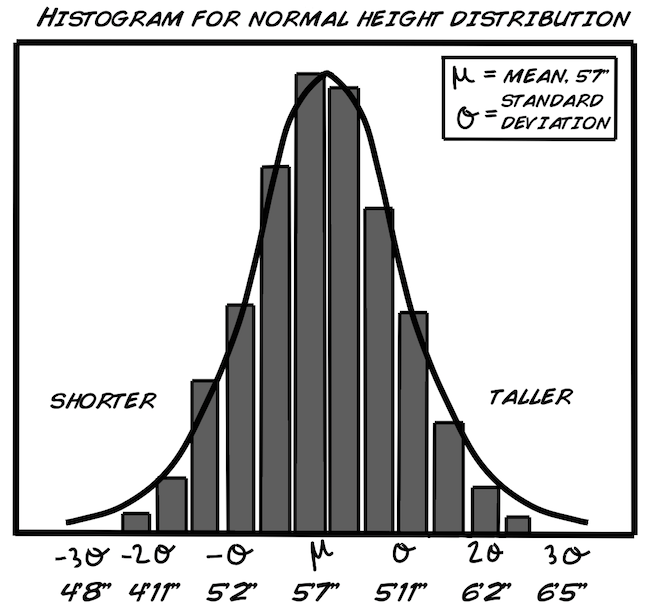
Keine Sorge wenn du sie nicht verstehst, aber Wissenschaftler haben herausgefunden, dass Körpergröße, IQ, Gewicht usw. normalverteilt sind. Deswegen nehmen wir an, dass Reaktionszeiten ebenfalls normalverteilt sind. Wir können uns das Beispiel der Körpergröße anschauen (Männer und Frauen kombiniert)
Die Verteilung der Größen macht den Datensatz "normal." Körpergröße hat einen zentralen Durchschnittswert und die Abweichungen verteilen sich symmetrisch um diesen Wert. In einer Normalverteilung:
Du denkst dir jetzt vielleicht, "Aber unsere Graphen sehen doch überhaupt nicht normalverteilt aus!" Da hast du zum Teil auch Recht, weil wir eine so kleine Stichprobe haben. Sobald wir die Stichprobengröße erhöhen würden (vielleicht bis auf 100), würden wir wahrscheinlich eine normalverteilte Kurve für unsere Reaktionszeiten bekommen, ähnlich zu der Kurve der Körpergrößen.
So, wie können wir jetzt testen, ob die beiden Datengruppen (beide von Rechtshändern: rechte vs. linke Hand) unterschiedlich sind? Dafür werden wir einen T-test durchführen, auch "Student's T-test" genannt. Der bekannte Dr. Student war ein richtiger Statistiker, aber "Student" war nicht sein echter Name. Der Name T-Test kommt von einer Aneinanderreihung witziger Ereignisse. William Gosset, ein Chemiker, der für die Guinness Beer Company in Irland arbeitete, entwickelte den Test 1908, um die Qualität der Bierzutaten zu testen. Er wollte den statistischen Test in einem Wissenschaftsmagazin veröffentlichen. Guinness hat ihm nicht erlaubt seinen echten Namen auf die Publikation zu schreiben, da sie die Analyse als Betriebsgeheimnis geheim halten wollten. Er bekam allerdings die Erlaubnis seinen Test unter einem Pseudonym zu veröffentlichen. Guinness hat dabei nicht bedacht, dass Gosset's Pseudonym (Student) unter den Wissenschaftlern bekannt war! Dank ihm, haben wir jetzt besseres Bier und bessere Statistik.
Der T-test ist mächtig, denn er erlaubt es uns Schlussfolgerungen aus einer Stichprobe für die gesamte Population zu ziehen. Wir werden dir zeigen wie man einen T-test für die erste Hypothese durchführt. Für die zweite Hypothese musst du aber selber ran!
Der T-test and die Analyse
Befor wir anfangen mit Zahlen um uns zu werfen, müssen wir eine exakt definierte Nullhypothese formulieren. Du fragst dich vielleicht warum wir zwei Hypothesen für einen statistischen Test brauchen. In der formalen Statistik, vergleichen wir immer zwei Hypothesen, die Null- und Testhypothese.
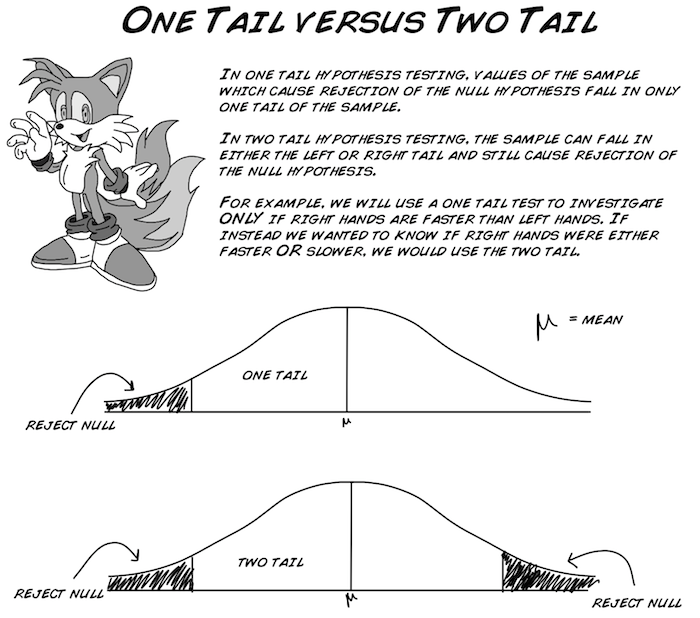
Jetzt müssen wir uns überlegen ob wir einen Einstichproben- oder einen Zweistichprobentest durchführen wollen. In unserer Analyse werden wir einen Einstichprobentest anwenden. Aus einem ganz einfachen Grund: uns interessiert es NUR ob die rechte Hand schneller als die linke Hand ist, nicht ob sie "schneller" ODER "langsamer" ist. Anders ausgedrückt: Falls es uns egal wäre, welcher Datensatz schneller war und wir uns nur anschauen wollen ob sie nicht den gleichen Mittelwert haben, würden wir einen Zweistichprobentest durchführen.
Zum Schluss müssen wir noch den "Alphawert" definieren. Man kann des Alphawert als "Annahmeschwellenwert" sehen. Am häufigsten werden die Werte .05, .01, und .001 verwendet. Bei einem Alphawert von .05, gibt es eine 95 prozentige Chance, dass deine Resultate korrekt sind. Bei einem Wert von .01, ist die Chance bei 99%... Dein Alphawert kann nie 0 sein! Da du dir in der Statistik nie 100% sicher sein kannst (das ist kein Witz!).
Der Alphawert ist weitläufig auch als "p-Wert" bekannt. Mit einem T-Test kannst du eine "T-Statistik" berechnen und sie mit einem bekannten "T-Wert" in einer Tabelle nachschauen. Jeder "T-Wert" ist mit einem "p-Wert" verbunden. Wenn deine "T-Statistik" größer ist als der nachgeschaute "T-Wert", dann kannst du die Nullhypothese verwerfen und aussagen, dass rechte Hände schneller sind als linke Hände! Verwirrt? Keine Sorge, wir wissen, dass es sich hier um ein komplizierten Prozess handelt und hatten selber einst Schwierigkeiten den "T-Test" zu verstehen.
So, jetzt bringen wir alle Datenpunkte, die wir bisher gesammelt haben, zusammen. Falls du dich an unsere Sektion: "Rohe Daten", Graphen & Verteilungen von oben erinnern kannst, haben wir folgende Werte bestimmt: Min(imum), Max(imum), Modus, Mittelwert, Standardabweichung und Median. Für den T-Test brauchen wir den Mittelwert, dei Standardabweichung und noch ein paar andere Werte, die wir unten berechnen werden.
Schritt 1: Finde die "zusammengeworfene Varianz", oder Sp^2.
Als nächsten setzen wir unsere Daten an die Stellen der Buchstaben in der oben genannten Formel.
Schritt 2: Berechne deine T-Statistik.
Jetzt haben wir unsere Varianz zusammengeworfen, Sp^2= .000119. Wir benutzen sie um die T-Statistik zu berechnen:
Hmm, was bedeuten nochmal die ganzen Buchstaben und Symbole? Wir kennen mittlerweile: Sp^2, n1 und n2. Aber was ist mit dem Rest?
Anmerkung: delta ist gleich null. Warum sollte die vorhergesagte Differenz unserer Datensatzmittelwerte null sein? KLEINER TIPP: Schau' nochmal auf deine Nullhypothese.
Und schon können wir austauschen. Bring' die Nummern in die Gleichung!
Unsere T-Statistik, t, ist .2046!
Schritt 3: Vergleiche deine T-Statistik mit den Werten in der T-Wert Tabelle
Wir vergleichen unsere berechnete T-Statistik mit der Standart T-Wert Tabelle. Du kannst sie entweder in Statistikbüchern finden oder hier: T-Wert Tabelle. Dafür brauchen wir noch "degrees of freedom=Freiheitsgrade", das df, was die Nummer unterschiedlicher Teile beschreibt, die FREI variieren.
Am Einfachsten kann man es sich mit einer Sportmannschaft vorstellen. Nehmen wir an du bist der Trainer und hast 11 Spieler, die du auf 11 Positionen einsetzen musst. Du wirst jeder Position den am Besten geeigneten Spieler zuweisen. Wie viele Entscheidungen musst du fällen? Nicht 11, 10!!. Sobald du den Spieler 10 einer Position zugeordnet hast, ist schon klar auf welcher Position der elfte Spiler spielen muss. Deswegen hattest du 10 Entscheidungen oder 10 Freiheitsgrade.
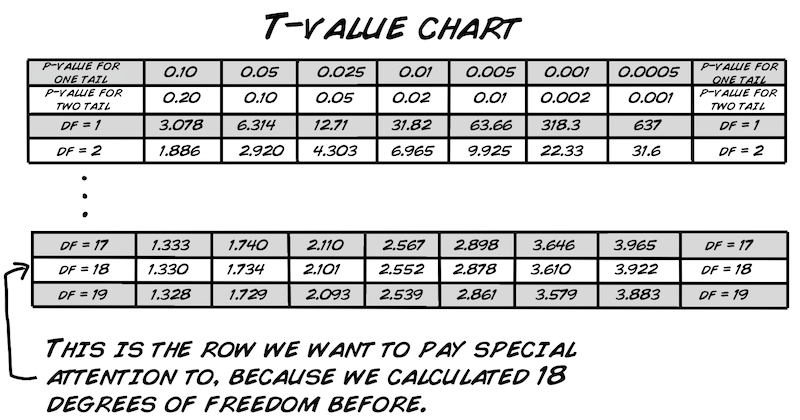
Geh' zur T-Wert Tabelle und schau' nach der Reihe mit dem df=18. Vielleicht fragst du dich grad: Wie zum Henker hat man diese Tabelle erstellt mit all' diesen zufällig erscheinenden Nummern. Gute Frage! Sie kann am besten mit der Integralberechnung der "Wahrscheinlichkeitsverteilung" erklärt werden. Wir haben oben das Thema bereits angeschnitten und frag' am Besten deinen Mathe Lehrer, wann ihr euch damit beschäftigen werdet...
Jetzt suche deinen p-Wert. Wir haben uns dazu entschieden, dass er bei 0.05 liegen soll und wir einen Einstichprobensignifikanztest durchführen. Zusammen mit unserem df=18 bekommen wir einen T-Wert von 1.734. Da unser berechneter T-Wert (0.2046) KLEINER ist als 1.734, KÖNNEN WIR NICHT die Nullhypothese verwerfen. Was wäre das Ergebnis bei einem nicht so "strengen" p-Wert, sag' mer mal 0.10?
Bei einem p-Wert von 0.10, bzw. 90% Konfidenz, ist unsere T-Statistik (0.2046) immer noch weniger als der Wert 1.330. Deswegen können wir immer noch nicht unsere Nullhypothese verwerfen, und ...
Wir können auch NICHT die Folgerung schließen, dass bei Rechtshändern rechte Hände schneller sind als linke Hände.
Es gibt also keine Indizien, dass du als Rechtshänder mit deiner dominanten Hand schneller reagierst als mit deiner "schwachen". Deswegen gehen WIR nun zu unserer 2. Hypothese über:
Sind Linkshänder mit ihrer linken Hand schneller als Rechtshänder mit ihrer rechten Hand?
Mit WIR meinen wir eigentlich DU. Du bist dran! Führe einen T-Test durch und berechne die Werte. Wir geben dir das Ergebnis vor. Die T-Statistik sollte 2.7187 sein. Bei einem p-Wert von 0.05 und dem Freiheitsgrad, df = 18, ist das ein größerer Wert als 1.734! Somit können wir mit 95%iger Konfidenz behaupten:
Linkshänder sind schneller als Rechtshänder.
Cool! Nachdem wir jetzt Resultate haben, können wir über sie diskutieren. Dieser Teil der Wissenschaft führt zu immer zu weiteren Fragen. Wenn Linkshänder schnellere Reaktionszeiten haben, dann sind sie vielleicht auch schlauer! Vielleicht können wir ja ein paar IQ Tests durchführen! Vielleicht kann man auch irgendwie ihre Nervengrößen messen, um herauszufinden ob sie eine schneller Leitgeschwindigkeit in ihren Nervenbahnen haben!
Unser nicht verworfene erste Hypothese ist um einiges schwieriger zu diskutieren. Vielleicht gibt es ja einen unterschied zwischen der Reaktionszeit der linken und rechten Hand bei Rechtshändern und wir haben nur nicht genügend Daten erhoben (dann hätten wir es mit einem Fehler 2. Art zu tun, auch "Stichprobenfehler" genannt). In der Wissenschaft ist es schwere zu beweisen, dass etwas NICHT da ist, als zu sagen, dass ein Effekt vorhanden ist. Alienjäger sagen gern: "Abwesenheit des Beweises heißt nicht gleich Beweis der Abwesenheit."
Du hast noch nicht genug?
- In unserem Experiment haben wir Freiwillige Teilnehmer untersucht und nicht zufällig 10 Testpersonen ausgewählt. Was ist da der Unterschied? Kann es sein, dass wir dadurch die Daten verfälschen? Was für einen Effekt hat unsere Wahl der Datenerhebung: verstärkt oder verschlechtert es unsere Schlussfolgerung? Oder machts eigentlich gar nichts?
- Kann man jemals sagen, dass eine Studie abgeschlossen ist? Was genau bedeutet 95% Konfidenz (Alphawert =0.05) für die "Wahrheit"?
- Fällt dir irgendetwas bei deinen Verteilungshistogrammen auf?
- Wir haben bisher nur die Reaktionsgeschwindigkeit der zwei Hände bei Rechtshändern getestet. Was würdest du bei Linkshändern erwarten? Probier's aus!